In the 12-note scale, when the basic chords (like a C major chord) are being formed, the sense of harmony is quite related with the integer #of characteristic waves that fits into longer waves (lower frequency, lower pitch).
Let’s consider the C-major (middle) chord: C4 E4 G4 C5 (do-mi-sol-do)
If the C4 is tuned to 261.63 Hz the wave length is .00382219164468906470 s. Lets calculate the frequencies of E4, G4 and C5. Initially note that two times the frequency (half the wavelength) is one octave higher in the scale (or half the frequency is one octave below).
A piano sound sample for C4
If we put 2 smaller waves in a single C4 wave:
.00382219164468906470 / 2 = .00191109582234453235 s
freq = 523.26 Hz
Sample of C4 and C5 together
If we put 3 smaller in a single C4 wave
.00382219164468906470 / 3 = .00127406388156302156 s
freq = 784.89 Hz
This is one octave higher. If we lower 1 octave (freq/2) -> 392.445 Hz
Sample of chord C4-G4-C5
If we put 5 smaller waves in a single C4 wave:
.00382219164468906470 / 5 = .00076443832893781294 s
freq = 1308.15 Hz
That is 2 octave higher. If we lower 2 octaves (freq/(2^2)) -> 327.0375 Hz
Sample of chord C4-E4-G4-C5
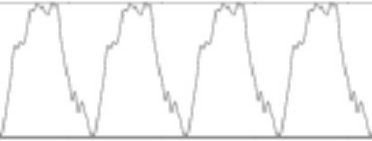
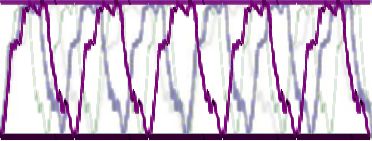
The above wave snippet shows only a timeframe of 15 milliseconds (0.0015 seconds). The human ear / mind cannot process this tiny wave separately and the hearing mechanism unconsciously perceives the wave alignment as “harmony” 
..
The contemporary frequencies for western music we have the following on a standard piano keyboard:
- C4 261.63 Hz
- E4 329.63 Hz
- G4 392.00 Hz
- C5 523.25 Hz
But the resulting frequencies are slightly different:
- C4 261.63 Hz
- E4 327.0375 Hz (-0.79% error)
- G4 392.445 Hz (0.11% error)
- C5 523.26 Hz (0.002% error)
This does not look perfect. Right? But well nothing is perfect .. See below:
Explanation of the Error Percentages
We should note that the errors below 1% are not noticeable to untrained ears at all where they are hardly noticeable to well-trained ears.
This basic mechanism is an implementation of the Pythagorean tuning which was a system of just (and mathematically perfect) intonation which tuned every note in a scale from a progression of pure perfect fifths (ratio of 3:2).
This was quite suitable for much of the harmonic practice until then, but in the Renaissance, musicians wished to make much more use of Tertian (C4-E(flat)4) harmony. The major third of Pythagorean tuning differed from a just major third by an amount known as Syntonic comma, which musicians of the time found annoyingly impure.
Syntonic Comma
In music theory, the syntonic comma, is a small interval between two musical notes, equal to the frequency ratio 81:80. Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. That stands as an error of 1.25% this is generally not noticeable.
Through Baroque, Renaissance era and 19th century there had been various temperaments used for the scales but today western music is based on the irregular temperament called Well Temperament.
Western Music Today – Well Temperament
“Well tempered” means that the twelve notes per octave of the standard keyboard are tuned in such a way that it is possible to play music in most major or minor keys and it will not sound perceptibly out of tune.
Summary
The C-major chord with contemporary (well) temperament:
- C4 261.63 Hz
- E4 329.63 Hz
- G4 392.00 Hz
- C5 523.25 Hz
is an acceptable approximation of mathematically perfect frequencies of 261.63, 327.0375, 392.445, 523.26 Hz chord with Pythagorean tuning.
Some text are copies from references below:
- http://en.wikipedia.org/wiki/Temperament_(music)
- http://en.wikipedia.org/wiki/Pythagorean_comma
- http://en.wikipedia.org/wiki/Syntonic_comma
- http://en.wikipedia.org/wiki/Well_temperament
- http://en.wikipedia.org/wiki/Meantone_temperament
